
0
Respost
How to add and hide references on diagram?
I have table A which is connected to many other entities, and I want to organize my diagram better.
So I drag the second copy of table A (the one with dashed borders) to the diagram. And I drag table B next to it. How can I draw an existing reference between these tables?
And how can I hide reference between original table A and table B? I don't want to delete the reference, I just want to hide its particular instance in the picture.
So I drag the second copy of table A (the one with dashed borders) to the diagram. And I drag table B next to it. How can I draw an existing reference between these tables?
And how can I hide reference between original table A and table B? I don't want to delete the reference, I just want to hide its particular instance in the picture.
Answer

Under review
As for references, some time ago one of our users has requested a new feature that looks quite similar to your idea.
He would like to have the option to hide all references in the model, leaving all the tables visible. If you'd like to hide selected references only, you can post your comment here:
http://support.vertabelo.com/topic/792344-option-to-hide-all-references-and-leave-only-tables-displayed/
You can also upvote this idea. The more votes the idea gets, the more likely it will be implemented.
He would like to have the option to hide all references in the model, leaving all the tables visible. If you'd like to hide selected references only, you can post your comment here:
http://support.vertabelo.com/topic/792344-option-to-hide-all-references-and-leave-only-tables-displayed/
You can also upvote this idea. The more votes the idea gets, the more likely it will be implemented.

Ok, so as for now it is not possible to hide references.
Can I move a single reference to be connected to another instance of the same table in the diagram?
Can I move a single reference to be connected to another instance of the same table in the diagram?

Answer
Respost
So I drag the second copy of table A (the one with dashed borders) to the diagram. And I drag table B next to it. How can I draw an existing reference between these tables?OK, you can do this with exactly 4 mouse clicks. First, select those tables (2 clicks). Then click on the reference symbol in the menu and choose "Show all references" option:
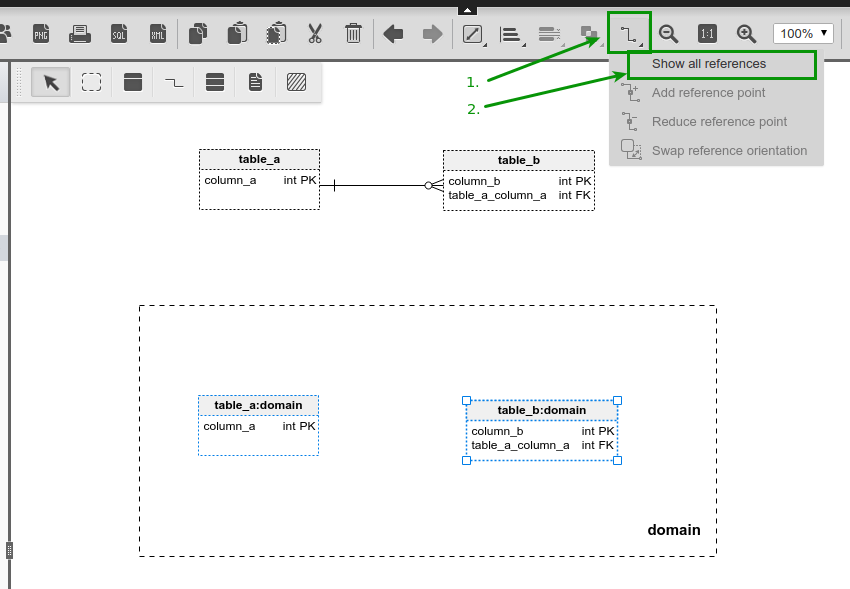
The reference will show up.
And how can I hide reference between original table A and table B? I don't want to delete the reference, I just want to hide its particular instance in the picture.If an object (table or reference) has more than one visual representation (has dashed borders), it's deletion is deletion of visual representation only. The model object is deleted when its last visual representation is deleted.
Customer support service by UserEcho


The reference will show up.
If an object (table or reference) has more than one visual representation (has dashed borders), it's deletion is deletion of visual representation only. The model object is deleted when its last visual representation is deleted.